[중1-1] 최대공약수와 최소공배수: 우리의 공통점과 차이점은?
안녕하세요?
이제 자기소개 시간이 끝나고,
가까운 자리의 친구들과 서로 이야기를 시작합니다.

12의 옆자리에 18이라는 친구가 앉았네요.
이야기를 하다보니 서로 공통점이 있다는걸 알았어요.
무슨 공통점일까요?
12 = 2×2×3
18 = 2×3×3
2와 3이 공통점이네요!
이렇게 숫자 친구 사이의 공통점을 공약수, 그 중 가장 큰 수를 최대 공약수라고 합니다.
반대로 차이점은 무엇인가요?
맞아요! 12는 2가 1개 더 있고, 18에는 3이 1개 더 있어요!
12와 18이 서로 가까워지기 위해서, 차이를 줄이고 싶어한다면 어떻게 해야 하나요?
12에는 3을 1개, 18에는 2를 1개 보충해 주면 될 것 같아요.
2×3×2×3 = 36
이렇게 만들어진 수는 36이 되고, 이를 최소공배수라고 합니다.
최대공약수 : 숫자들 사이의 공통점 중 가장 큰 수
최소공배수 : 숫자들 사이의 차이를 보완하는 가장 작은 수
여러분 주변의 친구들은 어떤 친구들인가요?
게임, 음악, 운동처럼 같은 관심사를 가지거나 비슷한 생각을 하는,
공약수가 큰 친구들도 있고,
관심사나 성격에 차이점이 있지만, 서로 이해하기 위해서 비슷해지려고 노력하는,
공배수를 같이 만들어 가는 친구들도 있을 거에요.
그럼 숫자 친구들의 최대공약수와 최소공배수를 구하는 방법은 무엇인지 알아보도록 할께요.

위 식에서 공통으로 나누어지는 2×3 이 최대공약수 6이 되고,
최대공약수로 나누어진 후의 차이가 되는 2와 3까지 포함하는 36 (6×2×3 = 36) 이 최소공배수가 됩니다.
예를 하나 더 들어볼께요. 24와 36의 최대공약수, 최소공배수 구하기입니다. (먼저 풀어 보고, 아래 답을 확인해보세요)
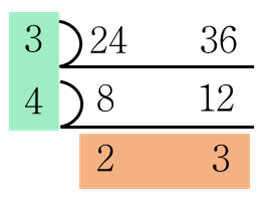
최대 공약수 : 12 (= 3×4)
최소 공배수 : 72 (= 12×2×3)
친구가 3명이나 4명인 경우는 어떻게 구할까요?
15, 25, 30 의 최대공약수와 최소공배수를 한 번 구해보겠습니다.
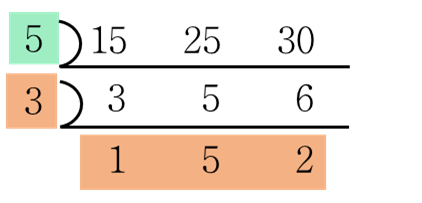
최대 공약수 (GCD) = 5
최소 공배수 (LCM) = 150 (= 5×3×1×5×2)
여기서 최대 공약수는 15가 아니라 모든 친구가 공통으로 가지는 수 5라는 점에 주의해주세요.
최대 공약수를 구하는데 몇몇 숫자들만 공통인 수를 계산하면 소외된 친구는 섭섭해 할 수 있겠지요?
반면, 최소 공배수를 구하는 과정에서는 몇몇 숫자들만 공통인 수 (3)로 나누는 이유는,
차이점을 중복해서 계산하지 않기 위해서 입니다. (그래서 "최소" 공배수에요)
잘 이해가 되셨는지 모르겠어요.
혹시 질문이 있으시면 댓글이나 방명록으로 글을 남겨주시면, 답변드리도록 하겠습니다.
그럼 다음 시간에는 지금까지 배운 것들을 정리해보고, 다양한 문제들을 풀어보도록 할께요.