안녕하세요.
지난 시간에 덧셈과 뺄셈을 배웠는데,
정수로만 계산을 하니 좀 부족했었던 것 같아요.
그래서! 이번엔 분수의 덧셈을 해보겠습니다.
(뺄셈은 덧셈과 같으니 따로 설명하지 않을께요.
자세한 내용은 이전 설명을 참조하세요 )
분수의 덧셈은 알고 계시겠지만 통.분.을 하면 됩니다.
분모를 통일시키는 건데요, 어떤 의미가 있는지 같이 살펴볼께요.
분수는 피자 조각으로 표현하면 참 좋은데요.
피자 1/2 조각과 1/3 조각,
\(\frac{1}{2}\) + \(\frac{1}{3}\) 을 표현하면 아래와 같습니다.
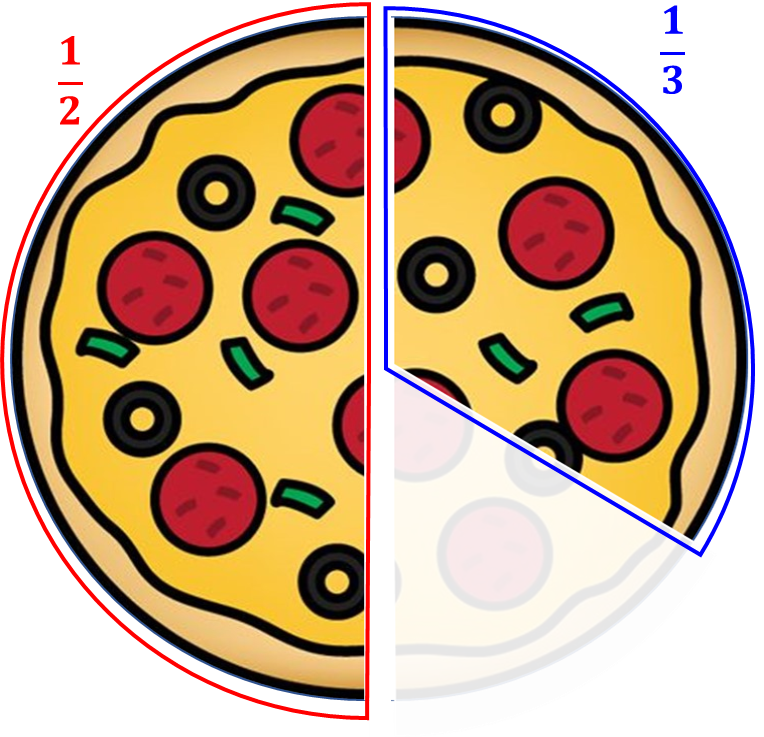
그런데 2등분과 3등분 조각이 서로 다르니, 계산이 안 되지요?
그래서 같은 크기로 잘게 나누어줍니다.
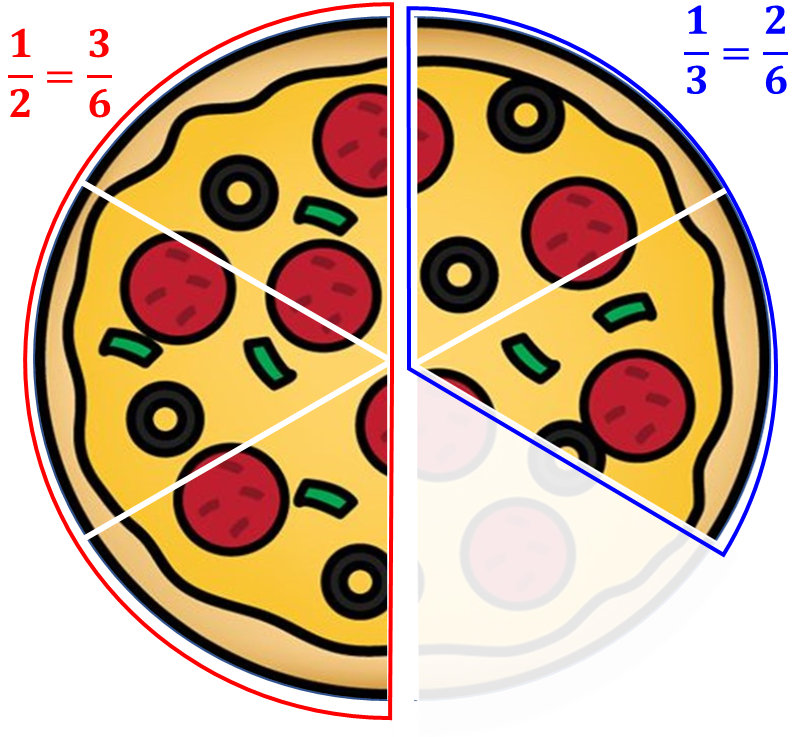
이제 크기가 같아졌으니, 정수의 덧셈처럼 계산해주면 됩니다.
\[\frac{1}{2} + \frac{1}{3} = \frac{3}{6} + \frac{2}{6} = \frac{5}{6} \]
\(\frac{1}{2}\) + \(\frac{1}{4}\) 은 어떻게 계산하면 될까요?
8조각으로 잘게 나누는 것보다는, 4조각으로 나누어도 같은 크기로 계산할 수 있겠지요?
\[\frac{1}{2} + \frac{1}{4} = \frac{2}{4} + \frac{1}{4} = \frac{3}{4} \]
따라서 통분을 할 때는 이와 같이 최소공배수를 사용합니다.
두 수 이상의 차이점을 포함한, 가장 작은 공통수를 찾는거지요.
최소공배수에 대해서는 여기를 참조하세요.
[중1-1] 최대공약수와 최소공배수: 우리의 공통점과 차이점은?
안녕하세요? 이제 자기소개 시간이 끝나고, 가까운 자리의 친구들과 서로 이야기를 시작합니다. 12의 옆자리에 18이라는 친구가 앉았네요. 이야기를 하다보니 서로 공통점이 있다는걸 알았어요.
huwan.tistory.com
통분이 끝난 분수의 덧셈과 뺄셈은 정수의 덧셈/뺄셈과 크게 다르지 않습니다.
음수나 뺄셈도 아래와 같이 통분을 하고, 분자에 대한 덧셈/뺄셈을 하시면 되겠습니다.
마지막에는 기약 분수로 표시하는 것을 잊지 마시고요.
\[\frac{3}{8} - \frac{1}{4} = \frac{9}{24} + (- \frac{6}{24} ) = \frac{3}{24} = \frac{1}{8} \]
\[\frac{5}{6} - \frac{9}{10} = \frac{25}{30} + (- \frac{27}{30} ) = (- \frac{2}{30} ) = (- \frac{1}{15} ) \]
다음은 곱셈과 나눗셈에 대해서 알아보겠습니다.
'중학수학' 카테고리의 다른 글
| [중1-1] 정수와 유리수: 계산의 순서 - 괄제곱더 (0) | 2022.07.04 |
|---|---|
| [중1-1] 정수와유리수: 곱셈과 나눗셈 (0) | 2022.05.08 |
| [중1-1] 정수와유리수: 덧셈과 뺄셈 (0) | 2022.04.24 |
| [중1-1] 정수와 유리수: 징검다리 (0) | 2022.04.17 |
| [중1-1] 정수와 유리수: 분수와 피자 (0) | 2022.04.11 |