안녕하세요?
지난 시간에는 소인수분해와 소수에 대해서 이야기해보았어요.
2022.03.18 - [중학수학] - [중1-1] 소인수분해 : 숫자의 자기소개 시간
[중1-1] 소인수분해 : 숫자의 자기소개 시간
안녕하세요? 수학을 어려워하는 친구들을 위해서, 제가 이해한 수학 이야기를 같이 나누어 보려고 합니다. 함께 하면서 질문이 있으면 댓글을 남겨주세요. 중학 수학의 첫 단원은 소인수분해인
huwan.tistory.com
소인수 분해는 숫자의 자기 소개 시간이라고 이야기를 했었죠.
그리고 12의 소인수분해를 통해서 12가 어떤 소수로 구성이 되어 있는지 살펴보았어요.
이번 시간에는 다른 숫자도 한 번 만나볼께요. 먼저 12와 가까운 친구인 24를 한 번 만나볼까요?
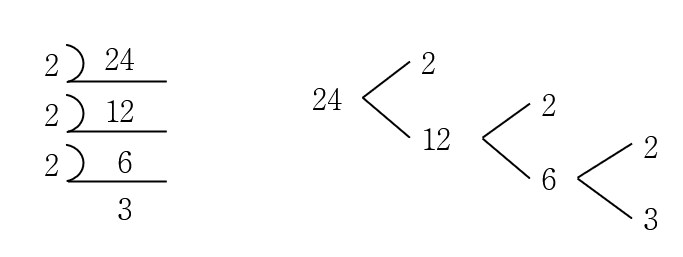
소인수분해 풀이는 위 방법을 참고해서, 자기가 가장 편하게 할 수 있는 방법으로 하면 됩니다.
이렇게 소인수분해를 통해서 24가 '2'가 3개, '3'이 1개로 구성된 합성수라는 것을 알 수 있어요.
24 = 2 × 2 × 2 × 3
그런데, 2가 여러 번 반복되니 한 눈에 읽기가 쉽지 않지요?
반복되는 수의 덧셈을 곱셈으로 바꾸는 것처럼,
반복되는 수의 곱셈을 지수로 표현할 수 있어요.
24 = \(2^3\) × 3
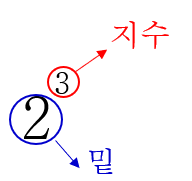
\(2^3\) 에서 '2' 를 밑 (base), '3'를 지수 (exponent) 라고 해요.
이번엔 여러분이 소인수분해를 해볼까요?
이번에 살펴볼 숫자는 32입니다.
(정답은 아래 "더보기" 에 있습니다.)
32 = 2 × 2 × 2 × 2 × 2 = \(2^5\) : 32는 2의 5제곱
앞으로 소인수분해는 계속해서 사용되기 때문에, 많은 연습이 필요해요.
다음에 나오는 수를 소인수분해 해보고, 정답과 비교해보세요.
: 27, 51, 78, 121, 144
27 = \(3^3\)
51 = 3 × 17
78 = 2 × 3 × 13
121 = \(11^2\)
144 = \(12^2\)
혹시 계산 속도가 느리거나, 실수가 많아서 속상한 분이 계신가요?
만약 좀 더 계산을 잘해보고 싶다는 마음이 있다면, 주변에 있는 숫자들에 자꾸 말을 걸어보세요.
: 시계나 달력에 보이는 숫자, 지나가는 버스나 자동차 번호, 친구 전화 번호, ...
그리고 너무 큰 수보다는 1에서 100사이의 수로 연습을 많이 하면 좋을 것 같아요.
아래에 나타난 숫자에 말을 걸어볼까요? (페이지 새로 고침을 하면, 숫자가 바뀝니다.)
연습을 통해 숫자와 좀 친해지셨다면,
다음은 여러 숫자들의 공통점과 차이점을 찾아 보는 최대공약수/최소공배수에 대해 알아보도록 하겠습니다.
'중학수학' 카테고리의 다른 글
| [중1-1] 소인수분해 : 단원 마무리 (0) | 2022.04.08 |
|---|---|
| [중1-1] 소인수분해 문제 : 약수의 개수 (0) | 2022.04.04 |
| [중1-1] 소인수분해 : 문제풀이 (0) | 2022.04.01 |
| [중1-1] 최대공약수와 최소공배수: 우리의 공통점과 차이점은? (0) | 2022.03.21 |
| [중1-1] 소인수분해 : 숫자의 자기소개 시간 (0) | 2022.03.18 |